How To Find Average Value Of A Function

How To Find Average Value Of A Function. For example, if the range a1:a20 contains numbers, the formula =average(a1:a20) returns the average of those numbers. These numbers are stored in the num[] array.

How do you find the average value of the function f(x from socratic.org

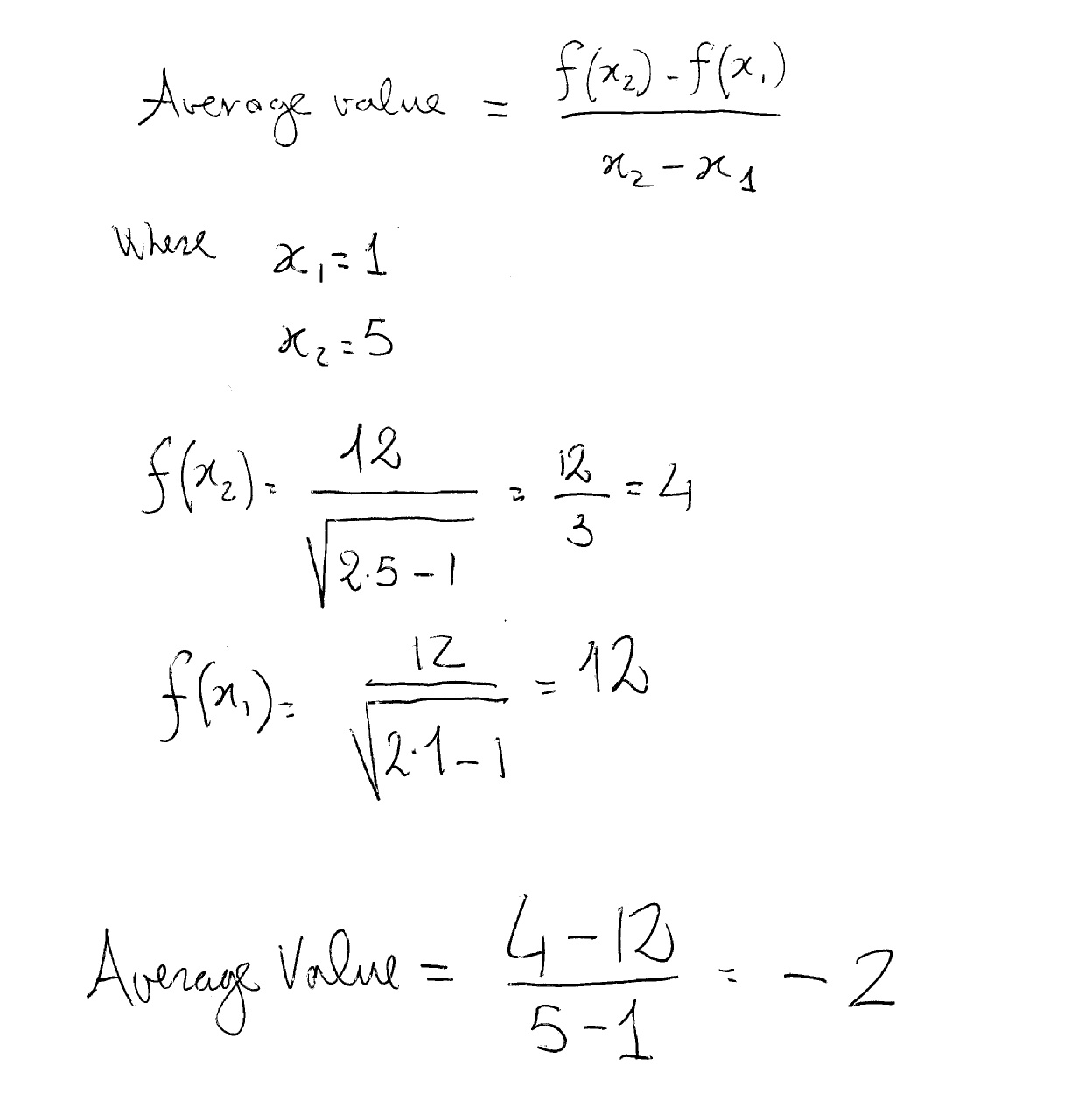
And, the sum of each entered element is computed. The formula we use to find the average value of a function f ( x) f (x) f ( x) over the interval [ a, b] [a,b] [ a, b] is. The most universally accepted average is the arithmetic mean, and excel uses the average function to find it.

Source: socratic.org

If that’s the case you’re in, it’s best to find an alternate function in. And, the sum of each entered element is computed.

Source: cochranmath.pbworks.com

U = 1 − cos ( 2 z) u = 1 − cos ⁡ ( 2 z) here is the average value of this function, r a v g = 1 π − ( − π) ∫ π − π sin ( 2 z) e 1 − cos ( 2 z) d z = 1 4 π e 1 − cos ( 2 z) ∣ ∣ ∣ π − π = 0 r a v g = 1 π − ( − π) ∫ − π π sin ⁡ ( 2 z) e 1 − cos ⁡ ( 2 z) d z = 1 4 π e 1 − cos ⁡ ( 2 z) | − π π = 0. Average value of a function definition of average value.

Source: www.youtube.com

Returns the average (arithmetic mean) of the arguments. ∫ f + f ( x) d x + ∫ f − − f ( x) d x b − a.

Source: www.youtube.com

Our average value of a function calculator gives you a step by step explanation to find average value of the given function. 9.4 average value of a function.

Source: www.youtube.com

The mean value theorem for definite integrals. For problems 1 & 2 determine \({f_{{\rm{avg}}}}\) for the function on the given interval.

Source: www.youtube.com

2450 / 9 = 271.11 The most universally accepted average is the arithmetic mean, and excel uses the average function to find it.

Source: www.nagwa.com

But let’s say you don’t want to take the average of all values, but only some specific ones. Our average value of a function calculator gives you a step by step explanation to find average value of the given function.

Source: www.youtube.com

Enter the average value of f (x), value of interval a and b in the below online average value of a function calculator and then click calculate button to find. 9.4 average value of a function.

Source: www.chegg.com

And, the sum of each entered element is computed. Note that,over the interval , the integral gives thetotal area of the region.

The Formula We Use To Find The Average Value Of A Function F ( X) F (X) F ( X) Over The Interval [ A, B] [A,B] [ A, B] Is.

U = 1 − cos ( 2 z) u = 1 − cos ⁡ ( 2 z) here is the average value of this function, r a v g = 1 π − ( − π) ∫ π − π sin ( 2 z) e 1 − cos ( 2 z) d z = 1 4 π e 1 − cos ( 2 z) ∣ ∣ ∣ π − π = 0 r a v g = 1 π − ( − π) ∫ − π π sin ⁡ ( 2 z) e 1 − cos ⁡ ( 2 z) d z = 1 4 π e 1 − cos ⁡ ( 2 z) | − π π = 0. 9.4 average value of a function. The average value of a function over an interval is given by the integral of the func.

Find The Average Value Of The Function.

👉 learn how to find the average value of a function using integration. Divide step 1 by the number of items in your set (9): How do we find the average of a set of numbers?

For Example, If The Range A1:A20 Contains Numbers, The Formula =Average(A1:A20) Returns The Average Of Those Numbers.

9.4 average value of a function. The average value of the function y = f(x) from x = a to x = b is given by: 2450 / 9 = 271.11

Then The Average Value Of | F | In [ A, B] Is.

The mean value theorem for definite integrals. Let y = f ( x) be a continuous function on the closed interval [. * (2 + 4 + 6) = 12.

The Most Universally Accepted Average Is The Arithmetic Mean, And Excel Uses The Average Function To Find It.

210 + 230 + 240 + 260 + 280 + 290 + 300 + 300 + 330 = 2450; But let’s say you don’t want to take the average of all values, but only some specific ones. ∫ f + f ( x) d x + ∫ f − − f ( x) d x b − a.